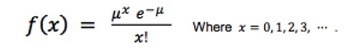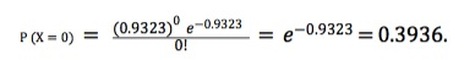χ2 Goodness of Fit Test of V2 Bomb Hits
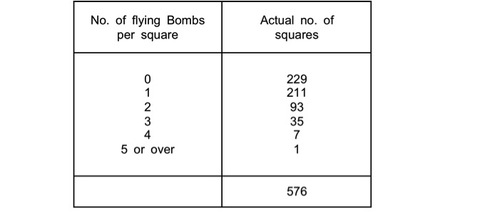
Over the period considered, the total number of fallen bombs within the 576 squares was 537. The actual results were as follow:
The average number of hits per square(μ) is then 537/576=.9323 hits per square. If the targeting is completely random, then the probability that a square is hit with 0,1,2,3 etc hits is governed by a Poisson distribution of which the probability distribution is as follows:
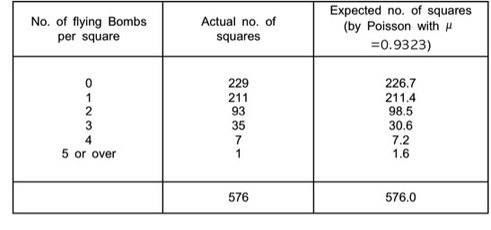
Then, the expected numbers of squares were calculated from the Poisson formula as the third column of the table below:
For instance, 226.7 in the third column can be obtained as follows:
Then, the predicted number(on average) of squares out of 576 in which there are no bomb hits Likewise, other numbers in the column 3 can be easily obtained.
The occurrence of clustering would have been reflected in the above table by an excess number of squares containing either a high number of flying bombs or none at all, with a deficiency in the intermediate classes. This is an instructive illustration: to the untrained eye, randomness appears as tendency to cluster.
To statistically test the actual fit of the Poisson for the data, a χ2 test to the comparison of actual with expected figures can be conducted as follows:
The occurrence of clustering would have been reflected in the above table by an excess number of squares containing either a high number of flying bombs or none at all, with a deficiency in the intermediate classes. This is an instructive illustration: to the untrained eye, randomness appears as tendency to cluster.
To statistically test the actual fit of the Poisson for the data, a χ2 test to the comparison of actual with expected figures can be conducted as follows:
Since 1.17 is much less than 13.3( , H0 cannot be rejected: the actual fit of the Poisson for the data is surprisingly good, which in fact lends no support to the clustering hypothesis(H1).
Notes
R. D. Clarke, “An Application of the Poisson Distribution,” Journal of the Institute of Actuaries, Vol. 72 (1946), p. 481; V-2 - Wikipedia, en.wikipedia.org/wiki/V-2; “London bombs: Poisson,” aurora.wells.edu/~srs/Math300.../Londonbombs.htm; Rick Cornez, Bombs of London, newton.uor.edu/FacultyFolder/Cornez/bomb.html.
Notes
R. D. Clarke, “An Application of the Poisson Distribution,” Journal of the Institute of Actuaries, Vol. 72 (1946), p. 481; V-2 - Wikipedia, en.wikipedia.org/wiki/V-2; “London bombs: Poisson,” aurora.wells.edu/~srs/Math300.../Londonbombs.htm; Rick Cornez, Bombs of London, newton.uor.edu/FacultyFolder/Cornez/bomb.html.